Zweifache Varianzanalyse

Für dieses Beispiel wird das Plugin 'RcmdrPlugin.iasc' benötigt.
In der empfohlenen vorbereiteten portablen Version ist das Plugin bereits automatisch geladen, Sie brauchen nichts weiter zu unternehmen.
Falls Sie jedoch R und das Plugin selbst installiert haben, können Sie den R Commander gleich mit dem aktivierten Plugin folgendermaßen starten: library("RcmdrPlugin.iasc")

Diese Seite beschreibt das Handling mit "R". Für Erklärungen zu den statistischen Inhalten besuchen Sie bitte die Vorlesung und die Übungen, und arbeiten Sie bitte Vorlesungs- und Übungsskripten durch.

Wie Sie CSV-Dateien importieren können, haben Sie bereits gelernt. Falls Sie sich nicht mehr erinnern, lesen Sie bitte nochmal nach: Dateneingabe und Einlesen von Beispieldateien. Um eine Varianzanalyse in R durchführen zu können, müssen die Daten in ein ganz bestimmtes Format gebracht werden. Ihre Tabelle muss so aufgebaut sein, dass

• jede Beobachtung in einer eigenen Zeile steht und
• jede Variable eine eigene Spalte erhält.

Sehen Sie sich die Datei 'Roggenversuch.csv' an. Sie enthält Daten über den Kornertrag (in dt/ha) verschiedener Roggensorten, einmal unter Beigabe von Steinmehl zur verwendeten Gülle, einmal ohne. Es wurden insgesamt 24 Beobachtungen durchgeführt, deshalb hat die Datei – inklusive der Spaltenüberschriften – 25 Zeilen. An jeder Beobachtung wurden drei Variablen erhoben, diese bilden die drei Spalten, wobei die Reihenfolge der Spalten unerheblich ist:

• sorte, das ist die erste Gruppierungsvariable (1. Faktor). Diese muss unbedingt den Datentyp Factor haben. Dieser Faktor hat die drei Stufen 'EhoKurz', 'Motto' und 'Kustro'.
• steinmehl, das ist die zweite Gruppierungsvariable (2. Faktor). Der Datentyp muss ebenfalls Factor sein. Dieser Faktor hat zwei Stufen 'mit' und 'ohne' und gibt an ob dem Dünger Steinmehl zugemischt wurde oder nicht.
• ertrag, das ist die kontinuierliche, metrische Variable (Zielvariable). Diese muss den Datentyp num oder int haben.

Sollten Sie Ihre Datei anders aufgebaut haben oder nach dem Einlesen der Daten ein falscher Datentyp vorliegen, wird der Menüeintrag zur "Mehrfaktoriellen Varianzanalye …" ausgegraut sein und Sie können keine Varianzanalyse durchführen. Haben Sie hingegen alles richtig gemacht, sollten Ihre Datenmatrix z.B. wie folgt aussehen:

Darüber hinaus muss auch der Datentyp der Variablen stimmen. Wie das überprüft werden kann ist im nachfolgenden Kapitel Struktur der Datenmatrix ermitteln beschrieben.

Tippen Sie in das Fenster 'R Skript' folgenden Befehl ein:

str(NameIhrerDatenmatrix)

und klicken Sie auf den Button 'Befehl ausführen'.

Zum Beispiel:

Die Variable, welche die kontinuierliche Zielgröße der Varianzanalyse bildet, muss natürlich numerisch sein, also den Datentyp int (integer, ganzzahlig) oder num (numerisch) aufweisen. Wenn die Zielgröße nicht numerisch ist, haben Sie bei der Dateneingabe oder beim Import Fehler gemacht.

Die beiden Gruppierungsvariablen, müssen zwingend Faktoren sein, also den Datentyp Factor aufweisen. Sollte eine der beiden Gruppierungsvariablen numerisch sein, muss diese Variable in einen Faktor umgewandelt werden.

Falls die Werte des Faktors numerisch sind, müssen diese unbedingt in Faktoren umgewandelt werden.
Wenn die Werte des Faktors aus Text bestehen, ist das nicht erforderlich.

'Datenmanagement' > 'Variablen bearbeiten' > 'Konvertiere numerische Variablen in Faktoren …'

Ein gruppierter Boxplot verschafft einen Überblick über die Daten. Leider bietet die normale Version des R-Commander nur die Möglichkeit gruppierte Boxplots mit einer einzigen Gruppierungsvariable zu erstellen. Für zwei Gruppierungsvariablen – wie im Fall der zweifaktoriellen Varianzanalyse sinnvoll – muss auf den Menüeintrag "Grafiken, Gruppierter Boxplot (2 Gruppen)" zurückgegriffen werden.

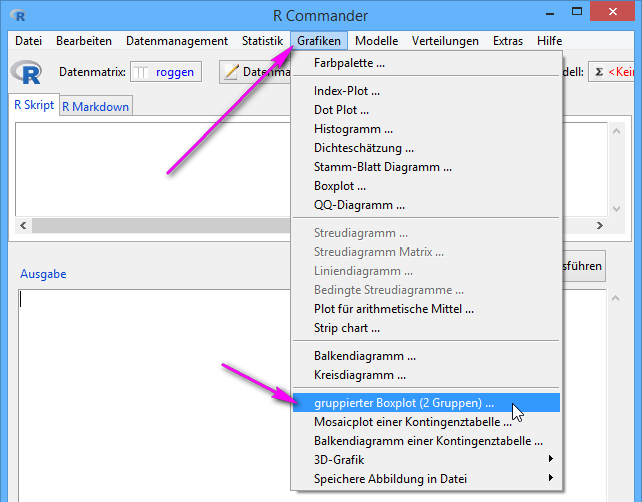
Falls Beschriftungen auf der x-Achse fehlen, machen Sie das Fenster bitte breiter, bis alle Beschriftungen Platz finden.

Bei kleinen Stichprobenumfängen ($n < 6$) ist ein Boxplot keine sinnvolle, grafische Zusammenfassung der Daten. Besser man stellt die beobachteten Stichprobenwerte selbst dar, z.B. in Form eines Stripcharts. Um zu verhindern, dass die Symbole von Beobachtungen übereinander gezeichnet werden, können Stripcharts "verrauscht" werden.

Den Schätzwert der Fehlervarianz erhält man, indem die Quadratsumme der Residuen (Sum Sq) durch die Anzahl der Freiheitsgrade dividiert werden. In dem obigen Beispiel errechnet sich die Fehlervarianz zu $29.052 / 18 = 1.614$.

Die Gleichheit der Varianzen wird mittels Levene-Test überprüft.

'Statistik' > 'Varianzen' > 'Levene-Test'

• Abgabe als PDF-Datei

• … fragen Sie bitte in der nächsten Übungseinheit Ihre Übungleiterin oder Ihren Übungsleiter.
• … fragen Sie auch Ihre Mitstudierenden, entweder persönlich in der nächsten Pause, oder im Forum des BOKUlearn-Kurses der Lehrveranstaltung. Bevor Sie im Forum fragen ...

Diese Seite beschreibt das Handling mit "R". Für Erklärungen zu den statistischen Inhalten besuchen Sie bitte die Vorlesung und die Übungen, und arbeiten Sie bitte Vorlesungs- und Übungsskripten durch!