Kontingenztafeln (Kreuztabellen)

Diese Seite beschreibt das Handling mit "R". Für Erklärungen zu den statistischen Inhalten besuchen Sie bitte die Vorlesung und die Übungen, und arbeiten Sie bitte Vorlesungs- und Übungsskripten durch!

In einer Marktuntersuchung einer Konsumentenschutzorganisation wurden 434 Testkäufe von Frischobst getätigt. Unter anderem soll geklärt werden, ob ein Zusammenhang zwischen Verkaufsform (Wochenmarkt, Einzelhändler oder Supermarkt) und Obstqualität (in drei Stufen: gut – mittel – schlecht) besteht.

         wochenmarkt haendler supermarkt
gut               65       69         30
mittel            27       82         73
schlecht          33       13         42

'Statistik' > 'Kontingenztabellen' > 'Analyse einer selbst eingegebenen Kreuztabelle …'

Ziehen Sie mit der Maus den Schieberegler nach rechts. Anzahl der Zeilen: 3; Anzahl der Spalten: 3

Geben Sie Zeilen- und Spaltenüberschriften und Häufigkeiten ein:

         wochenmarkt haendler supermarkt
gut               65       69         30
mittel            27       82         73
schlecht          33       13         42

Klicken Sie auf den Reiter 'Statistik', und haken Sie 'Zeige erwartete Häufigkeiten' an:

In der Tabelle ist die erwartete Häufigkeit angegeben. Der p-Wert der dazugehörigen Teststatistik ($1.95\cdot10^{-11}$) liegt unter dem Risiko 1. Art $\alpha = 0.05$, weshalb die Nullhypothese abgelehnt werden muss. Es besteht also ein Zusammenhang zwischen Verkaufsform und Qualität.

Der gefunden Zusammenhang kann mittels gruppiertem Balkendiagramm veranschaulicht werden.

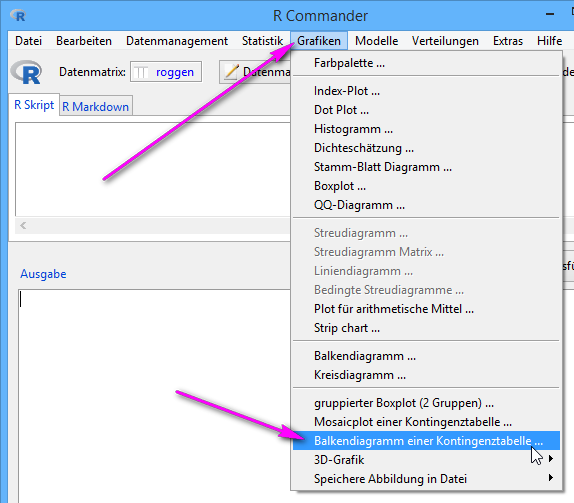
Wählen Sie bitte Menüpunkt 'Grafiken' > 'Balkendiagramm einer Kontingenztabelle …'

Bei Zutreffen der Nullhypothese erwartet man ein gleichartiges Bild der Säulengruppen. Deutliche Abweichungen – wie in diesem Fall – stehen dagegen im Widerspruch zur Nullhypothese. Man erkennt gut, dass beim Händler schlechte Qualität eine geringere Rolle spielt, wohingegen im Supermarkt gute Qualität eindeutig unterrepräsentiert ist.

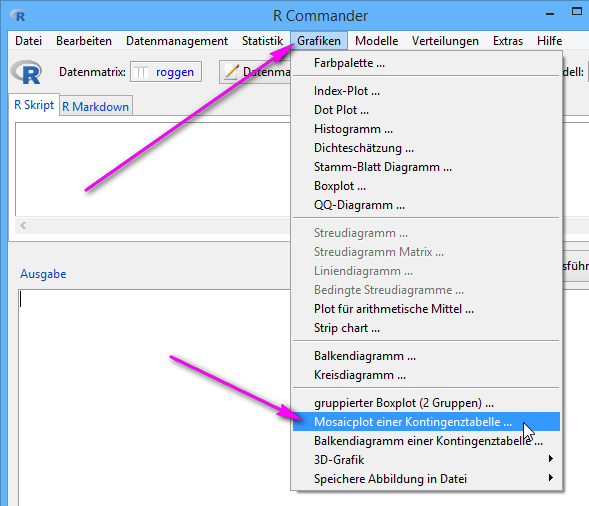
'Grafiken' > 'Mosaicplot einer Kontingenztabelle …'

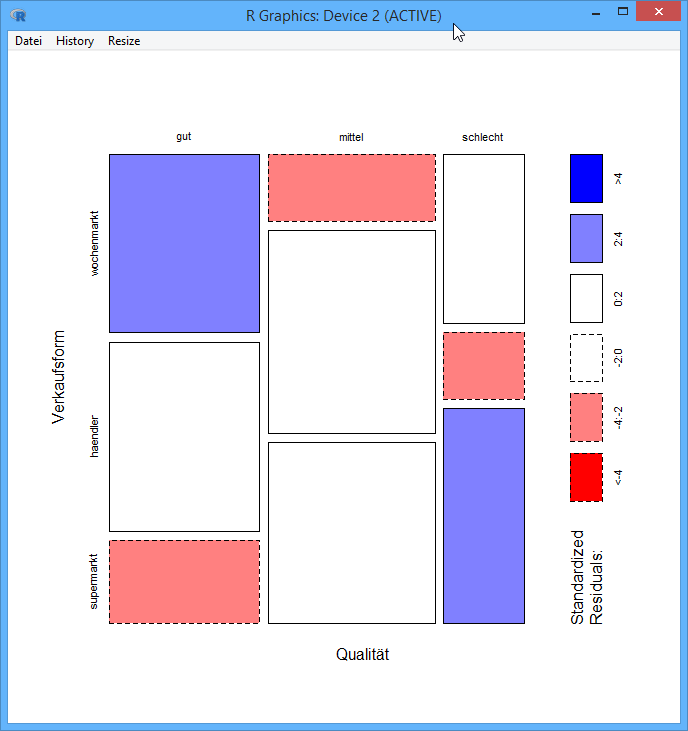
Die eingefärbten Zellen markieren Abweichungen von der Nullhypothese Unabhängigkeit: Blaue Zellen sind größer als man sie bei Unabhängigkeit erwarten würde, hier gute Qualität im Wochenmarkt (links oben) und schlechte Qualität im Supermarkt (rechts unten). Umgekehrt sind rote Zellen kleiner als unter Unabhängigkeit erwartet, z.B. gute Qualität im Supermarkt (links unten).

• Abgabe als PDF-Datei

• … fragen Sie bitte in der nächsten Übungseinheit Ihre Übungleiterin oder Ihren Übungsleiter.
• … fragen Sie auch Ihre Mitstudierenden, entweder persönlich in der nächsten Pause, oder im Forum des BOKUlearn-Kurses der Lehrveranstaltung.

Diese Seite beschreibt das Handling mit "R". Für Erklärungen zu den statistischen Inhalten besuchen Sie bitte die Vorlesung und die Übungen, und arbeiten Sie bitte Vorlesungs- und Übungsskripten durch!